Which functions have an additive rate of change of 3? Select two options.

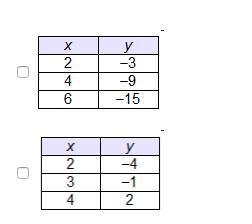
Answer

Functions that have an additive rate of change of 3 include linear functions like f(x)=3x+2 and g(x)=3x−1. These functions increase by 3 units in their output for every unit increase in their input. The slope of each function confirms this constant rate of change.

Explanation

To determine which functions have an additive rate of change of 3, we need to look for functions that exhibit a constant increase of 3 units in the output (y-values) for every increase of 1 unit in the input (x-values). This means that if we take any two points on the function, the difference in the y-values will always equal 3 times the difference in the x-values.

For instance, consider the following functions:

An example is the function defined as:

f(x)=3x+2

Here, for every increase of 1 in x, the output f(x) increases by 3. This satisfies the additive rate of change of 3.

2. Another Linear Function:

Another example is:

g(x)=3x−1

Similarly, this function increases by 3 for every increase of 1 in x, confirming the additive rate of change is also 3.

In both cases, the slope of the function is 3, indicating the additive rate of change is constant. Therefore, both f(x)=3x+2 and g(x)=3x−1 are functions that exhibit an additive rate of change of 3.